Path Planning
“Bézier Curves have useful properties for path planning" (Choi, Curry and Elkaim, 2009, p. 1):The curve “always passes through the first and last control point” (Dixit and Silakari, 2015, p. 319) as the first and last control points are interpolated and the interior control point(s) approximated.
This property will allow me to easily define the first control point with the foot position at the start of swing phase, and the fourth control point as the desired end position as the double support phase begins – leaving the interior control points to define any features of the trajectory including step height or obstacle avoidance.
Shown in Figure 1, another beneficial property is these curves will “always lie within the convex hull of their control points” (Choi, Curry and Elkaim, 2009, p. 1). Because Bernstein polynomials (used in calculation of the curve) are nonnegative between 0 and 1 and must all sum to unity, the polyhedron made by all four control points of a Bézier curve will contain the complete curve. This guarantees the curve will both never have oscillations outside of the control points internal area.
 |
| Figure 1: Cubic Bézier curve within the convex hull of it’s control points (Al-Shemary, 2009, p. 38) |
The variation diminishing property of Bézier curves also means that the curve cannot intersect with itself unless this would also occur by linearly interpolating between the consecutive control points, as noted by Weisstein.
These behaviours effectively remove any risk of undesirable fluctuations in plotted trajectory, unless the solution defines the control points configuration to purposefully accomplish this.
As discussed by Agoston (2005, p. 404), Cubic Bézier curves exhibit no local control. Any change made to any of the control points will require recalculation of the whole curve, though the further the control point is from an area of the curve, the less it will be affected by any change to the control point.
Global control will be of benefit to my solution as the first and last control points will not be amended once the end position has been defined. Updating the entire curve if the interior control points are repositioned to allow for obstacle avoidance, rather than a single section, will maintain a more natural trajectory (compared to undulation during the swing phase which does not occur in human gait).
Implementation
A Bézier curve is defined by 2 or more control points.Regardless of the parametric degree (dictated by the number of curve control points) any Bézier curve can be calculated given the parametric function:
 |
| Figure 2: Bézier curve parametric function (Lengyel, 2012, p. 322) |
Linear Bézier Curve
Shown in figure 3, the curve is drawn by linearly interpolating between two control points, using an incremental value (t) between 0 and 1. The value represents the proportional position along the curve (e.g. if the value is halfway between 0 and 1, the current curve position will be halfway between the control points). |
| Figure 3: Interpolation over time of linear Bézier curve (Wikipedia Contributors, 2018) |
I do not wish to draw the curve over time when used as part of IK solution, so increment t within a for loop to calculate and draw all curve positions each frame.
 |
| Figure 4: Function to draw linear Bézier curve within for loop |
On each loop t is divided by the resolution of the curve to interpolate its value between 0 and 1.
The limit check of the for loop compares against the curve resolution value plus one, to ensure the final point in curve will be drawn at the final control points position.
The position of each point is then defined by calling the CalculateLinearCurvePoints function.
To show the drawn curve I added functions to display both the point positions themselves (green spheres) and connecting segments (white lines).
 |
| Figure 5: Function to calculate linear resolution point positions |
The resulting curve:
 |
| Figure 6: My linear Bézier curve implementation |
Quadratic Bézier Curve
Shown in figure 7, a quadratic curve is calculated by linearly interpolating between two linear Bézier curves.Figure 8 demonstrates this process over time. Pairs of adjacent control points are used to calculate linear Bézier curves, which are then used to linearly interpolate to produce the quadratic curve.
 |
 |
| Figure 7: Interpolation of a quadratic Bézier curve (Al-Shemary, 2009, p.38) | Figure 8: Interpolation over time of a quadratic Bézier curve (Wikipedia Contributors, 2018) |
I used the same for loop logic as for the linear curve implementation to call a function to compute the curve positions using three control points.
 |
| Figure 9: Function to calculate quadratic resolution point positions |
The result:
 |
| Figure 10: My quadratic Bézier curve implementation |
Cubic Bézier Curve
Shown in figure 11, a cubic curve is calculated by linearly interpolating between two quadratic Bézier curves.Figure 12 demonstrates this process over time.
 |
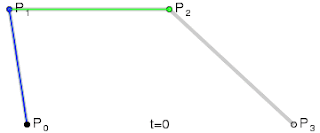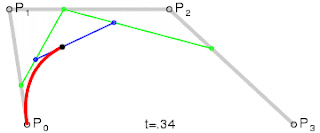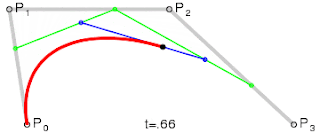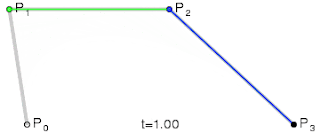 |
| Figure 11: Interpolation of a cubic Bézier curve (Al-Shemary, 2009, p. 38) | Figure 12: Interpolation over time of a cubic Bézier curve (Wikipedia Contributors, 2018) |
Using the same logic as used for the previous curves, I again created a new function to calculate the curve positions using four control points.
 |
| Figure 13: Function to calculate cubic resolution point positions |
The result:
 |
| Figure 14: My cubic Bézier curve implementation |
As the same equations apply to a 3D space, having used Vector3 allows the implementation to work along the z-axis too.
 |
| Figure 15: My cubic Bézier curve implementation, 3D |
The cubic curve performs as expected from my earlier reading, demonstrating the properties discussed.
One issue I was not able to solve was creating all curve positions exactly from the initial control point to the final control point, due to how the for loop increments the interpolation value. This means that while C1 continuity is still present for all point positions throughout the curve, the first point position calculated is placed one increment value from the first control point.
The significance of this gap can be reduced by increasing the resolution of the curve by adding more curve position points.
If I choose to continue development with cubic Bézier curves, this is not likely to be an issue as my current IK solution has a dampened seek behaviour, so any movement will remain smooth regardless of whether the gap remains present.
References
Agoston, M. (2005). Computer graphics and geometric modelling. London: Springer, pp.558-563, 674-796.
Al-Shemary, M. (2009). Analysis of Bézier Method Numerically with Applications. Master of Science. University of Kufa. Available at: https://www.researchgate.net/publication/313360210_Analysis_of_Bezier_Method_Numerically_with_Applications [Accessed 17 Dec. 2018]
Choi, J., Curry, R. and Elkaim, G. (2009). Obstacle avoiding real-time trajectory generation and control of omnidirectional vehicles. 2009 American Control Conference, [online] p.1. Available at: https://www.researchgate.net/publication/224561370_Obstacle_avoiding_real-time_trajectory_generation_and_control_of_omnidirectional_vehicles [Accessed 25 Dec. 2018].
Dixit, M. and Silakari, S. (2015). Utility of Parametric Curves in Image Processing Applications. International Journal of Signal Processing, Image Processing and Pattern Recognition, [online] 8(7), p.317-321. Available at: https://pdfs.semanticscholar.org/7fd7/e5697dff423a35987b23904c899037738b83.pdf [Accessed 24 Dec. 2018].
Lengyel, E. (2012). Mathematics for 3D Game Programming and Computer Graphics. 3rd ed. p.317-329.
Shabeeb, A. (2013). Path Planning of Robot Manipulator Using Bezier Technique. Degree of Master of Science. University of Technology (Iraq). Available at: https://www.researchgate.net/publication/311936981_path_planning_of_robot_manipulator_using_bezier_technique [Accessed 25 Dec. 2018].
Weisstein, E. (n.d.). Weisstein, Eric W. "Convex Hull." From MathWorld--A Wolfram Web Resource.. [online] Mathworld.wolfram.com. Available at: http://mathworld.wolfram.com/ConvexHull.html [Accessed 27 Dec. 2018].
Wikipedia Contributors (2018). Bézier curve. [online] En.wikipedia.org. Available at: https://en.wikipedia.org/wiki/B%C3%A9zier_curve [Accessed 27 Dec. 2018].
Bilbiography
Breen, D., Regli, W. and Peysakhov, M. (n.d.). Hermiteand Catmull-Rom Curves. Available at: https://www.cs.drexel.edu/~david/Classes/CS536/Lectures/L-04_Hermite_Catmull_Rom.6.pdf [Accessed 26 Dec. 2018]
Choi, J. and Elkaim, G. (2008). Bezier Curve for Trajectory Guidance. Proceedings of the World Congress on Engineering and Computer Science 2008, [online] pp.1 - 5. Available at: https://www.researchgate.net/publication/252576833_B_ezier_Curve_for_Trajectory_Guidance [Accessed 24 Dec. 2018].
Mehdi, S., Choe, R. and Naira, N. (2015). Avoiding Multiple Collisions through Trajectory Replanningusing Piecewise B ́ezier Curves. 2015 IEEE 54th Annual Conference on Decision and Control (CDC), [online] pp.2755-2760. Available at: https://ieeexplore-ieee-org.uos.idm.oclc.org/stamp/stamp.jsp?tp=&arnumber=7402633&tag=1 [Accessed 26 Dec. 2018].
Sellarès, T. (n.d.). Curves. Available at: http://ima.udg.edu/~sellares/MEG/CurvesMEG09.pdf [Accessed 26 Dec. 20189]
Zhou, F., Song, B. and Tian, G. (2011). B ezier Curve Based Smooth Path Planning for Mobile Robot. Journal of Information & Computational Science 8: 12 (2011) 2441–2450, [online] pp.1 - 10. Available at: https://www.researchgate.net/publication/285739464_Bezier_curve_based_smooth_path_planning_for_mobile_robot [Accessed 19 Dec. 2018].
George, G., Moitra, A., Caculo, S. and Prince, A. (2018). Efficient Architecture for Implementation of HermiteInterpolation on FPGA. [online] pp.7 - 11. Available at: https://ieeexplore-ieee-org.uos.idm.oclc.org/stamp/stamp.jsp?tp=&arnumber=8596920 [Accessed 26 Dec. 2018].